Sphero control

2016-06-10 00:00:00 +0000

Overview

This project was part of the course ME 454, Optimal Control of Nonlinear Systems, at Northwestern University. The goal of the project was to design an optimal trajectory for the Sphero robot to escape from a concave surface by oscillating back and forth. Without the speed of the oscillation, the Sphero is unable to escape the concavity.

Dynamics

We formulated the dynamics using the Lagrangian of the system and the Euler-Lagrange equation. Our state consisted only of the angle with respect to the center of the bowl and the angular velocity with respect to the center of the bowl. We did not consider movement outside of the plane.

$L = -g*m*(R_{sphere} - cos(\theta(t))*(R_{sphere} - r_{ball})) + \frac{inertia*R_{sphere}^2*\omega(t)^2}{2*r_{ball}^2} + \frac{1}{2} m*R_{sphere}^2*\omega(t)^2$

The three terms represent potential energy due to the changing height and kinetic energy due to linear velocity and rotational velocity.

The Euler Lagrange equation and dynamics were then as follows:

$\dot \omega (t) = \frac{g*m*sin(\theta (t))*r_{ball}^2*(r_{ball} - R_{sphere})}{(inertia+m*r_{ball}^2)*R_{sphere}^2}$

We estimated values for the radii and inertia, and attempted to find a straight line trajectory for the ball using the iLQR method. We also changed the ratio of the input acceleration term to the system acceleration term to accommodate the dynamics. While we could run the algorithm for a couple of iterations, we were never able to achieve reasonable tracking with these dynamics. We therefore simplified the system to only include the linear velocity term, reasoning that we could scale the results.

Cost Function

Our original intention for the cost function was to specify a desired final angular position and limit the velocity using barrier functions to see if the algorithm could independently come up with a way to achieve this. This didn’t work as planned, as our logarithmic barrier functions caused integration errors in Mathematica with imaginary numbers. Different attempts to fix this caused undesirable results with negative costs and Mathematica warnings. We therefore used a cost function minimizing path error.

Design

We initially set the desired state as a sine wave to test whether an oscillatory path would be appropriate for the dynamics of the system. While the robot could execute this path, it wasn’t quite the behavior we wanted.

The second path chosen was an increasing sine wave of the form tsin(t) that was scaled accordingly. This seemed a more appropriate choice because the objective of the Sphero was to try moving up the curvature of the chair by rolling back and forth and building momentum which is similar to an increasing sine wave function. However, this posed problems because the Sphero’s velocity is limited by its mechanics and could not overcome friction at the low speeds we requested of it.

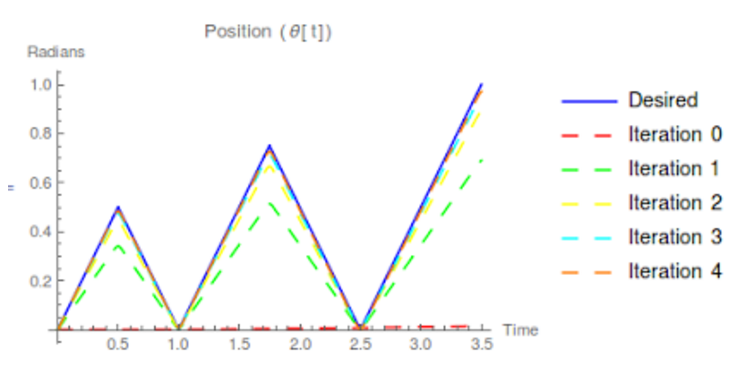
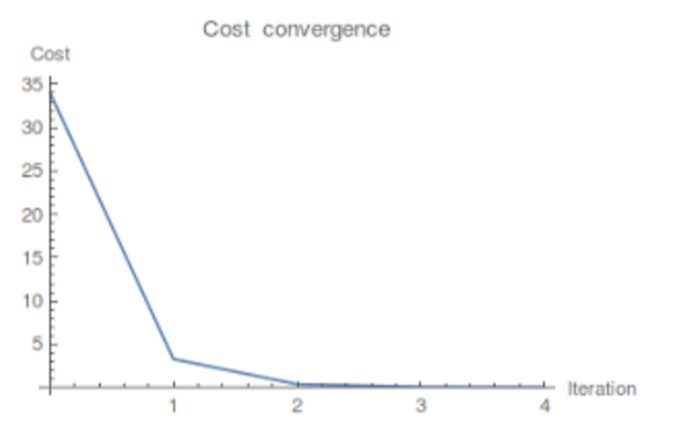
Finally, we assumed a piecewise function for the desired angular velocity of the sphero and integrated it to obtain the desired position. A Piecewise function seemed logical since the Sphero’s goal is to instantly switch directions and oscillate on the curvature. Adopting this desired state resulted in quick convergence and better behaviors than the previous options discussed above. The cost convergence plot as well as the state plots are detailed in the next section.

Solution

With these choices of dynamics, cost, and desired state, the iLQR method was able to converge much faster than in our various experimentations, and we arrived at an optimal state trajectory very close to the desired trajectory. The following plots depict the variation of the state through every iteration. The algorithm was run for a total of 5 iterations.