Kinodynamic Trajectories

2016-03-15 00:00:00 +0000

Overview

The main goal of this project was to generate kinodynamic trajectories using an RRT to release a ball so it would land at a desired location. This was a semester-long project at Northwestern University. The task is split into 5 main components:

All of the code for this project is hosted on this page.

See a demo of the robot throwing a ball to three distinct positions here:

See another demo of the robot throwing the ball from flexible starting positions:

This implementation relies on work from the following sources:

Zhang, Yajia, Jingru Luo, and Kris Hauser. “Sampling-based motion planning with dynamic intermediate state objectives: Application to throwing.” Robotics and Automation (ICRA), 2012 IEEE International Conference on. IEEE, 2012.

S. M. LaValle and J. J. Kuffner. “Randomized kinodynamic planning”. Proc. IEEE Int’l Conf. on Robotics and Automation, 1999.

Hauser, Kris, and Victor Ng-Thow-Hing. “Fast smoothing of manipulator trajectories using optimal bounded-acceleration shortcuts.” Robotics and Automation (ICRA), 2010 IEEE International Conference on. IEEE, 2010.

Sánchez, Gildardo, and Jean-Claude Latombe. “On delaying collision checking in PRM planning: Application to multi-robot coordination.” The International Journal of Robotics Research 21.1 (2002): 5-26.

Release state sampling

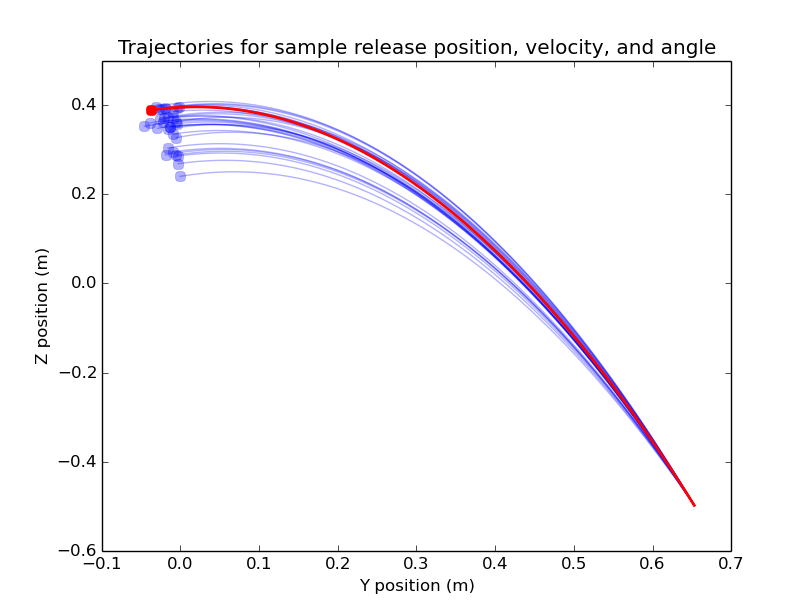
This task samples object release points and velocities at random that will send the ball on a ballistic trajectory to the target point. This release state is tested for solvablity using inverse kinematics and tested for velocity bounds.

An example is shown below of 30 sampled release points and their trajectories; the chosen release point is highlighted in red.

Kinodynamic RRT

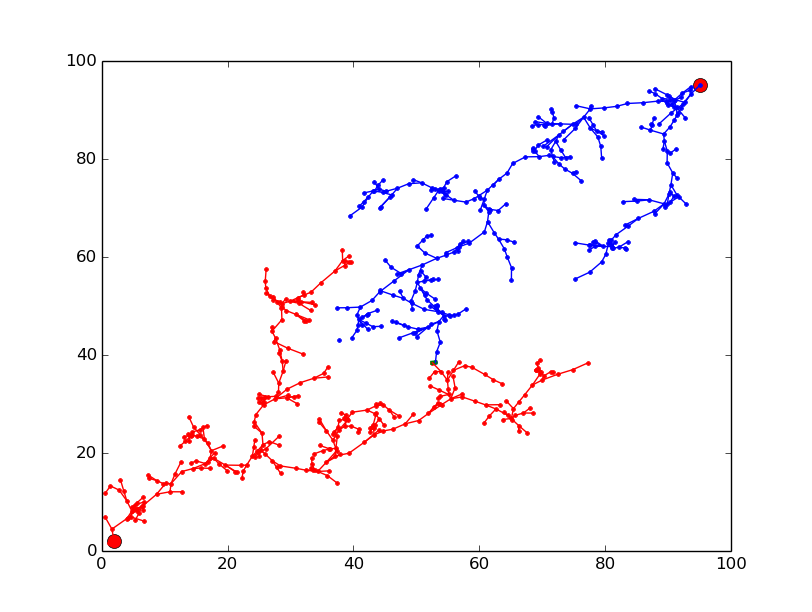
This task finds a path from a given start position and velocity to the sampled position and velocity for each of Baxter’s seven joints while obeying physically-based dynamic models and avoiding position and velocity limits. This approach is tailored to trajectory planning in high-dimensional state spaces and is therefore a good approach for the 14-DOF system. It utilizes a bidirectional RRT to speed up the sampling process.

An example is shown below for a 2-DOF system using a bidirectional kinodynamic RRT and the resulting path.

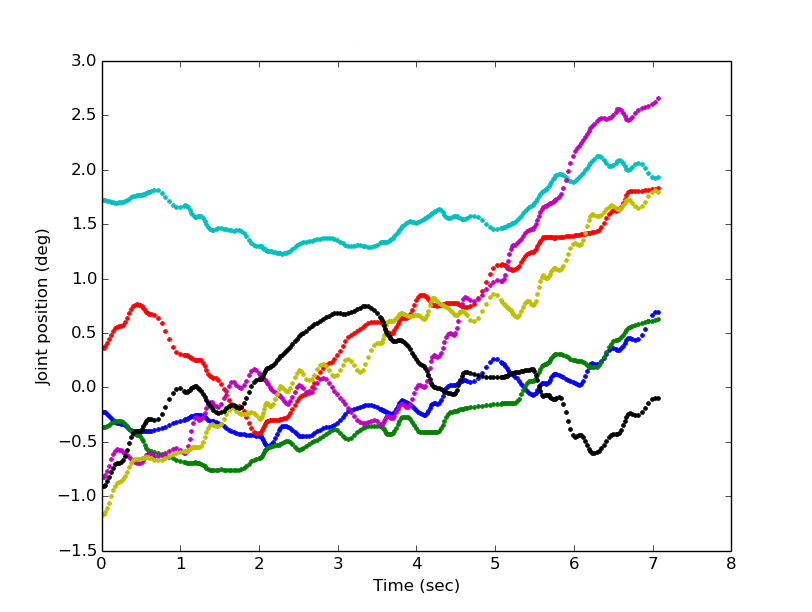
When extended to 14-DOF, the RRT results in paths like the one below which shows positions for each of the 7 joints over time.

Lazy collision checking

Once a path has been found that connects the start and release states with a dynamically feasible trajectory, collisions are checked for each point along the path. The planner is lazy in that the path is found prior to collision checking as collision checking tends to be the most computationally intensive constraint to check. Collision checking uses the built in service from MoveIt!.

Path smoothing

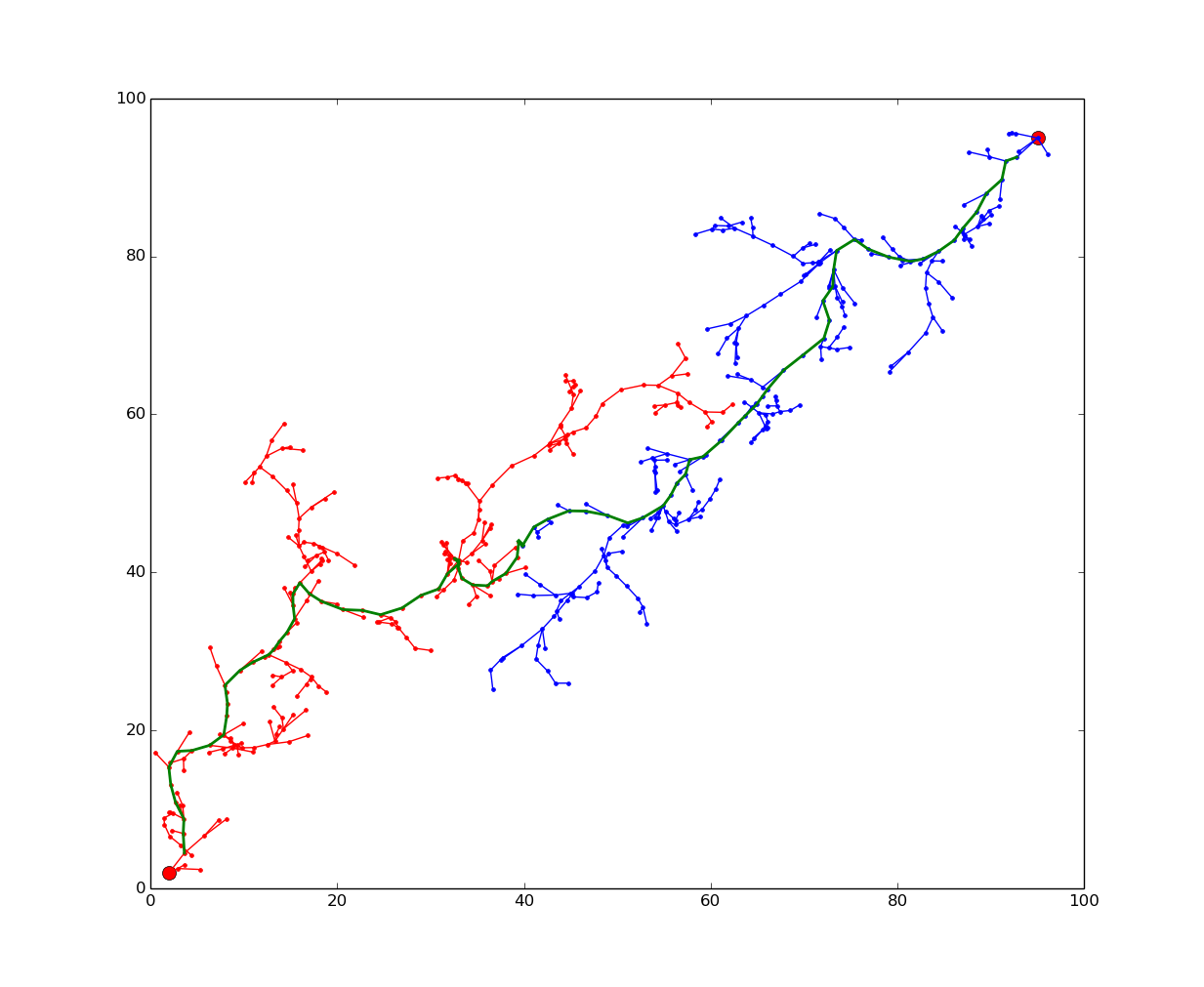
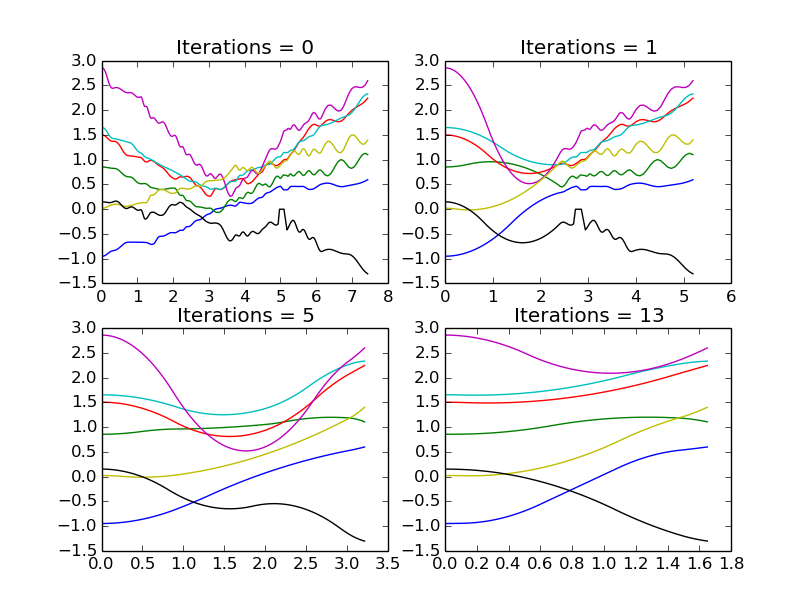
This task employs a shortcutting method to smooth jerky trajectories for high DOF manipulators subject to collision constraints, velocity bounds, and acceleration bounds. This algorithm first converts the path to a trajectory over time using a 5th order spline that respects state conditions and velocity and acceleration limits. The shortcutting algorithm is then employed over 30 iterations: for each iteration, two random states are picked from the trajectory. The minimum execution time is determined by the slowest single-joint trajectory using the fastest dynamically feasible trajectory between joint states. Once this time has been determined, the rest of the joints are interpolated for this time using the minimum-acceleration interpolant. This new segment replaces the old segment only if the overall time for execution has been reduced.

Below is an example of the shortcutting method over 30 iterations. It smooths the path and reduces the overall time.

Performance

From the nominal starting position, the throwing accuracy is about 8 out of 10. From a flexible starting position, the accuracy is much worse. The inconsistency is a problem beyond the scope of this project, as there is no clear relationship between the path and the time of the release, and this is the largest perceived source of error. An effort is being made to use machine learning algorithms to figure out which starting conditions and path correspond to the highest accuracy.

Important nodes

• check_rrt_joint.py iterates through RRT and path smoothing and sends results to the collision checker
• check_state_for_collisions.py sends joint lists to the collision service provided by MoveIt! and returns state validity
• path_smooth.py converts a path into a timed trajectory and smooths the path with shortcuts
• release_state_sample samples release states for projectile motion
• release_state_solve checks release states using IK and velocity bounds
• rrt_joint.py uses a kinodynamic RRT to calculate a path from start position to release position
• throw_path.py sends a path to the joint trajectory action server for execution

Dependencies

• Baxter SDK - follow the Workstation Setup Instructions
• pykdl_utils package - clone this repository
• urdf package with apt-get install ros-version-urdfdom-py
• kdl package with apt-get install ros-version-kdl-conversions

Instructions for running files

To run the files, the workspace must be connected to Baxter and properly sourced. Then use the following command: roslaunch baxter_throw throw_demo.launch. In the input_state window, enter 1, 2, or 3 to move the box to one of three set positions which Baxter will throw to.